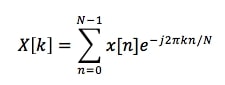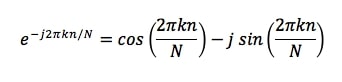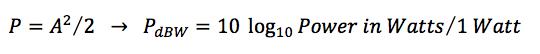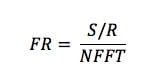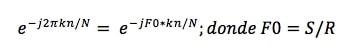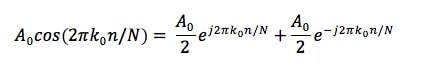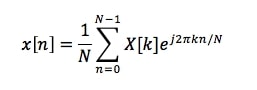Los técnicos de sonido obtienen datos de medición pero, ¿como se toman y cuales son sus limitaciones? Instalia presenta el anàlisis de la representación espectral por Pepe Ferrer, ingeniero de sistemes audiovisuales.
La representación espectral
Afortunadamente, hoy en día se ha convertido en habitual que los técnicos de sonido utilicen herramientas de medición y análisis para desarrollar sus diseños o ajustes. Obtener la repuesta en frecuencia de un sistema, comparar respuestas de fase o visualizar la respuesta impulsional de una sala está al alcance de la mano para cualquier profesional del audio. Obtenemos datos que nos ayudan a tomar decisiones, pero en muchas ocasiones desconocemos como éstos son tomados y cuáles son sus limitaciones. En este artículo estudiaremos como a partir de la transformada de Fourier, en nuestro caso la discreta, convertimos la información temporal de una señal en sus correspondiente respuesta espectral.
La Transformada Discreta de Fourier
Esta es la ecuación más importante que debemos conocer si estamos interesados en profundizar en el conocimiento del análisis en el dominio discreto.
Donde n = índice temporal discreto (muestras), k = índice discreto en frecuencia, N = tamaño de la DFT y x[n] = la señal de entrada, nuestra serie de entrada de muestras discretas. En la ecuación podemos observar como multiplicamos cada muestra de la señal por una exponencial compleja. Es decir, a partir de la DFT encontramos la cantidad de exponenciales complejas que contiene la señal que estamos analizando.
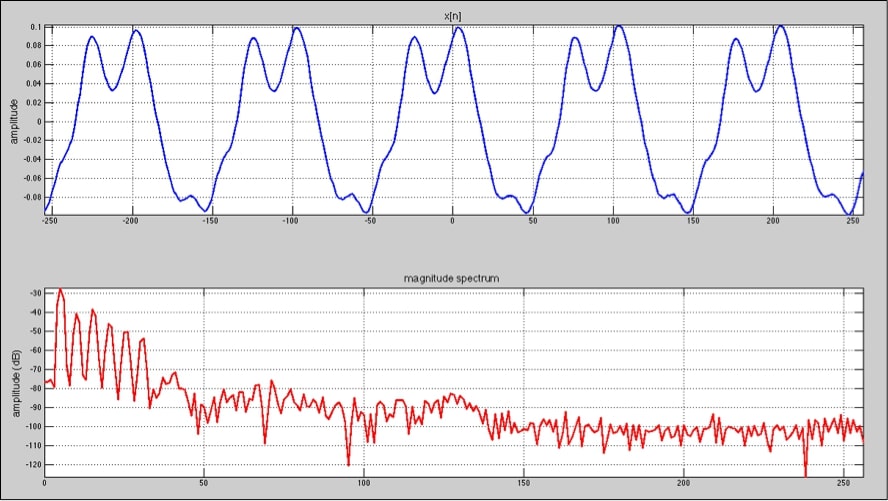
Veamos un ejemplo, la señal de entrada es un sonido de flauta, y analizamos una porción de 512 muestras:
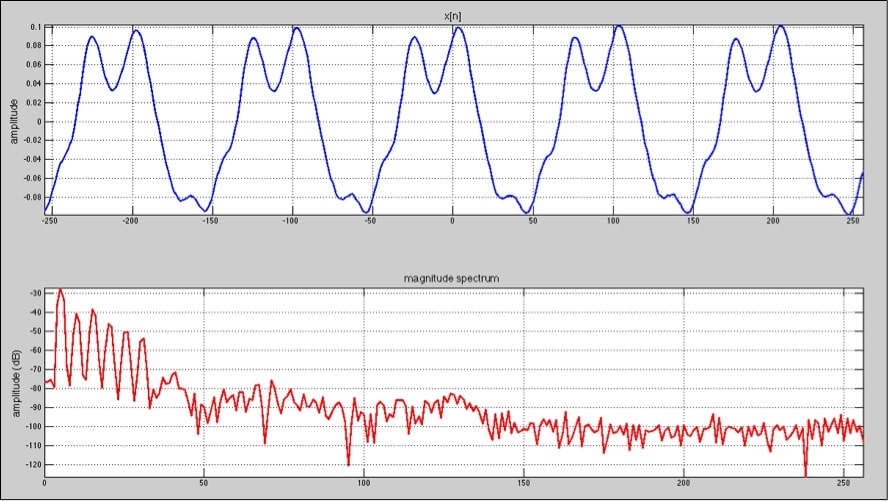
Si nos fijamos detalladamente en el gráfico podemos observar como la señal temporal es cortada en 512 muestras y en su respuesta espectral solamente visualizamos 257 muestras, la mitad del tamaño de la DFT que hemos usado (512) y la frecuencia cero, es decir, hemos graficado la parte positiva de la respuesta. Explicaremos esto con más detalle en breve.
En el gráfico de la respuesta espectral visualizamos las frecuencias que forman la señal en un eje de abscisas lineal. Podemos observar que se trata de una señal armónica.
Exponencial Compleja
Al aplicar la DFT, la señal de entrada se ve multiplicada por una serie de exponenciales complejas, ondas sinusoidales complejas, que forman la base del análisis. Las transformada nos devolverá la información de cual son las exponenciales complejas que están presentas en la señal.
Como ya hemos comentado en varios artículos anteriores, una exponencial compleja está formada por una parte real y otra imaginaria y que la identidad de Euler nos permite descomponerla en un coseno y en un seno:
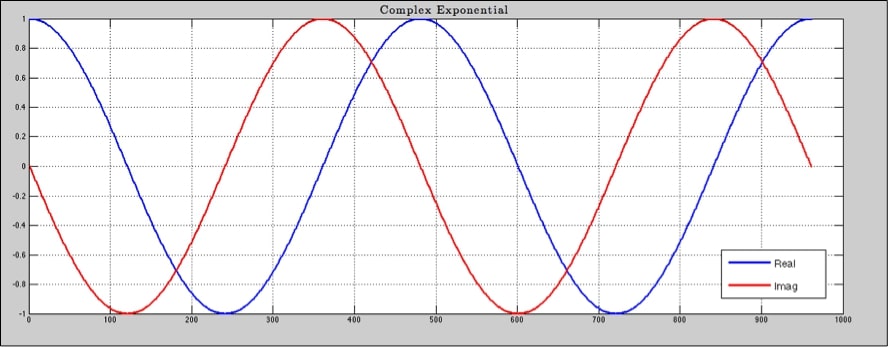
Veamos su funcionamiento. Analizamos un fragmento de 16 muestras de una señal de audio. Por lo tanto, como máximo podremos encontrar 16 sinusoides complejas:
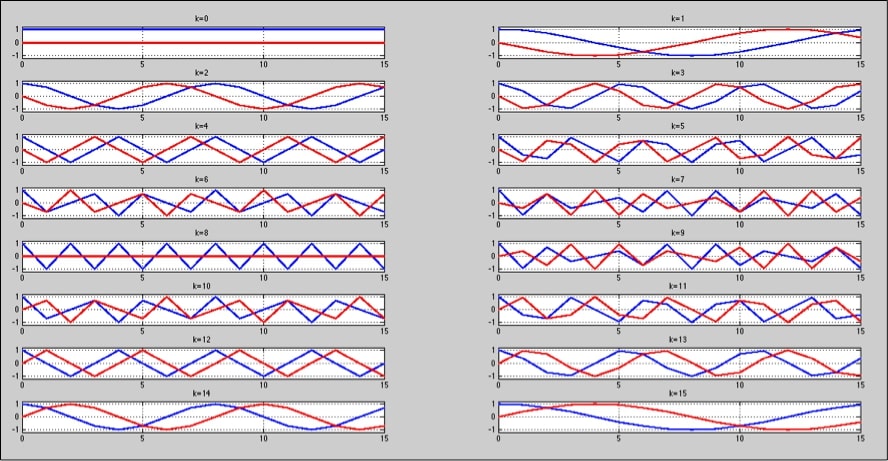
Si nos fijamos en detalle en el gráfico, vemos que la frecuencia 0 equivale al componente DC de la señal y a partir de ahí cada incremento equivale a un periodo más, es decir, para k=1 tenemos un ciclo de un coseno (parte real) y un ciclo de un seno (parte imaginaria), k=2, 2 ciclos y así sucesivamente hasta llegar a K=8 donde se invierte el resultado y disminuye un ciclo a medida que aumenta el valor de la sinusoide. También se puede observar la simetría.
¿Qué quiere decir esto? Pues que si calculamos la DFT a un fragmento de una señal de 16 muestras, éstas son las sinusoides que vamos a poder localizar.
A medida que aumentamos el tamaño del fragmento a analizar mayor numero de sinusoides podremos localizar, lo que significa que vamos a poder obtener una mayor resolución frecuencial.
Calculemos la DFT de 128 muestras para una sinusoide compleja de 16 ciclos:
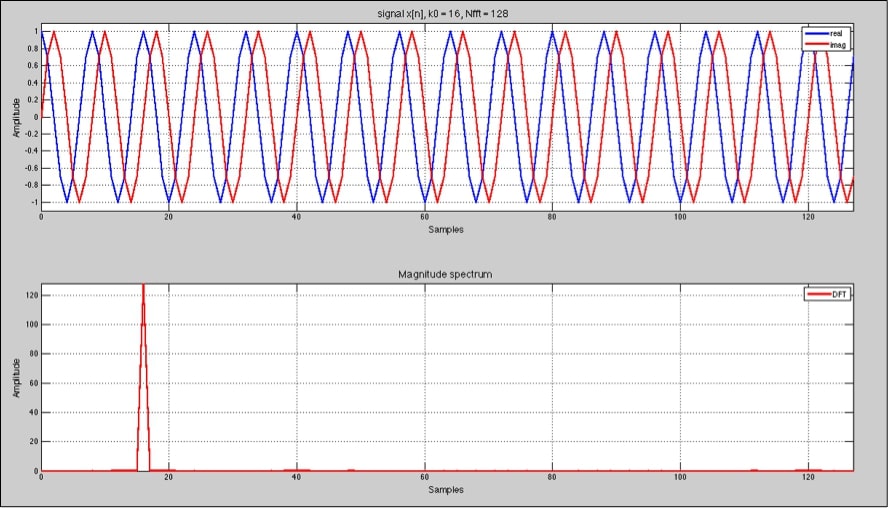
Al aplicar la transformada a una señal que coincide con una de las sinusoides que son base de la DFT, el resultado nos muestra que el contenido en frecuencia es cero para todos los componentes base excepto para dicha frecuencia, y que su amplitud es 128, que coincide con el tamaño de la DFT. Podemos definir la DFT como la proyección de la señal en un conjunto finito de sinusoides complejas. La DFT nos permite identificar cuantas de ellas están presentes en la señal.
Veamos el mismo ejemplo en el analizador RiTA. En este ejemplo RiTA toma la potencia de la señal. Para una sinusoide con amplitud de 1V, la potencia de la parte positiva del espectro en Watts es dada por la siguiente ecuación:
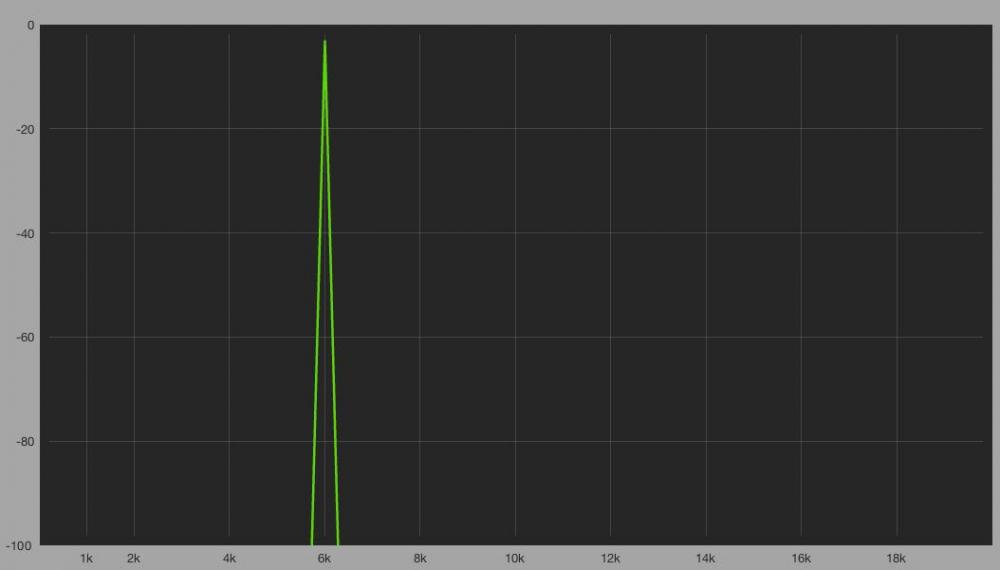
En este ejemplo, la señal de entrada coincide con una de las frecuencias exactas que la DFT puede localizar, pero esto no es lo habitual, lo habitual es que los componentes de la señal de entrada no coincidan con un múltiplo exacto de la frecuencia de resolución.
Recordemos que la frecuencia de resolución de un analizador depende de la frecuencia de muestreo y el tamaño de la DFT:
Para los ejemplos estamos tomando las frecuencias normalizadas, pero en cualquier momento podemos conocer el valor de la frecuencia aplicando la siguiente sustitución:
Veamos qué ocurre al aplicar el mismo tamaño de DFT que el ejemplo anterior pero para una señal de entrada de 15.5 ciclos:
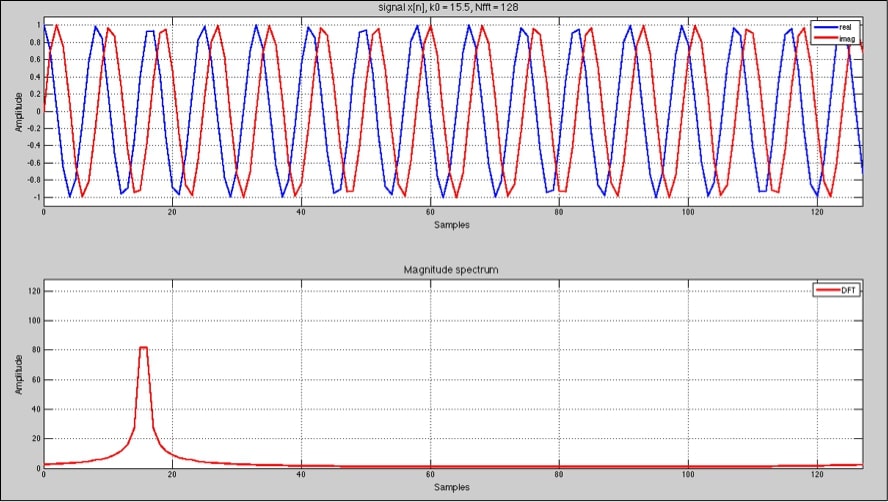
15.5 periodos no corresponde a un valor entero, es decir, no tenemos una señal que tenga un número de periodos entero dentro de las 128 muestras que estamos analizando. Si observamos con atención el gráfico, podemos comprobar que todos los valores de frecuencia son positivos, y la mayor amplitud se centra alrededor de 15.5. En este caso el valor para la muestra 15 y 16 tienen la misma amplitud. El analizador no puede mostrar correctamente el valor de la señal de entrada y reparte la amplitud entre los valores más próximos:
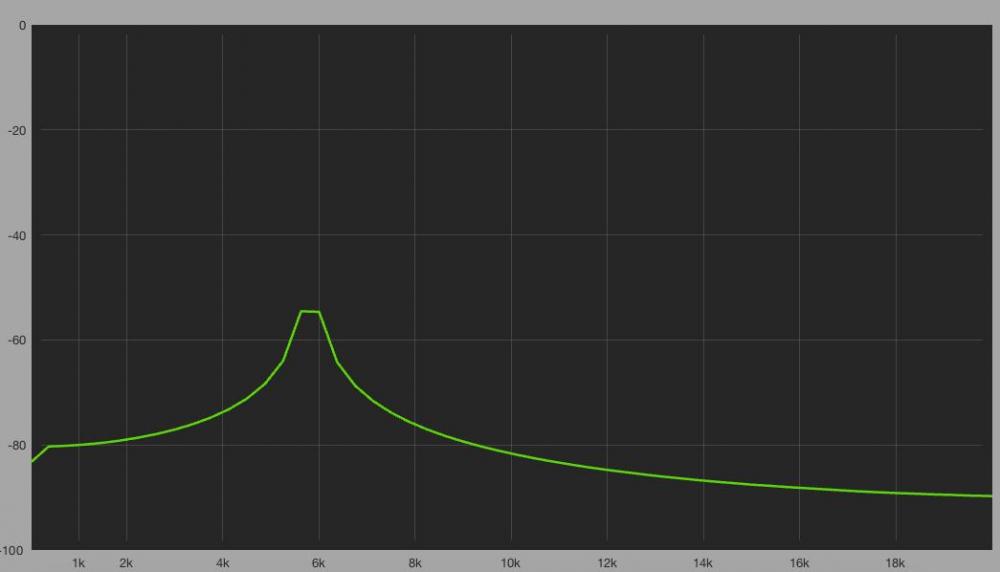
Podemos observar el mismo efecto en la respuesta de RiTA, pero truncada para visualizar el espectro positivo.
Señales Reales
En el anterior apartado hemos visto cómo un analizador nos muestra aplicando la DFT el contenido de sinusoides complejas que están presentes en la señal, pero en el mundo real nosotros no nos encontramos con señales complejas, sino que manipulamos y analizamos señales reales.
Entonces, ¿cómo podemos realizar la DFT de una señal real?. Sabemos por la identidad de Euler que cualquier sinusoide real se puede expresar como la suma de dos sinusoides complejas:
Por lo tanto, si aplicamos la DFT a una señal real, el resultado es básicamente 2 DFTs, una de frecuencia positiva y otra de frecuencia negativa:
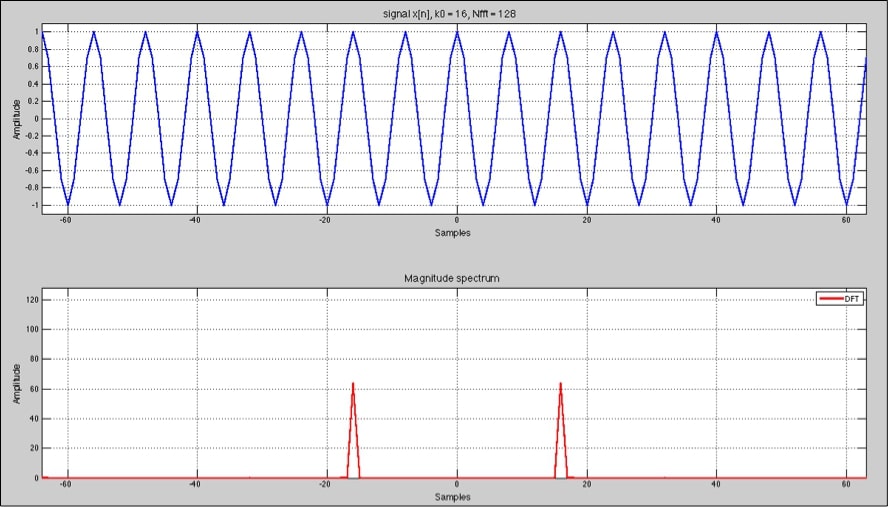
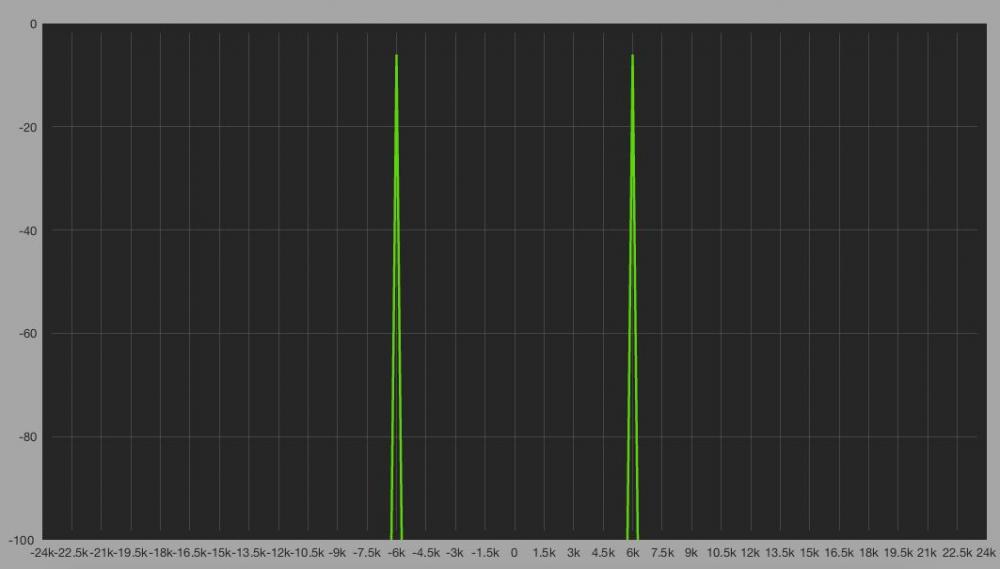
Como podemos observar en la medición aparecen dos frecuencias, una situada en la parte negativa y la otra en la parte positiva del espectro. La amplitud de ambas respuestas como sabemos por la ecuación de Euler corresponden a la mitad, en este caso 64 que es la mitad del tamaño de la DFT que hemos usado 128 muestras. Recordad que disminuir la mitad de potencia expresado de modo logaritmico significa reducir 3dB.
Por lo tanto, cuando analizamos en un analizador la respuesta al espectro de una señal, únicamente visualizamos la parte positiva y normalmente expresado en dBW.
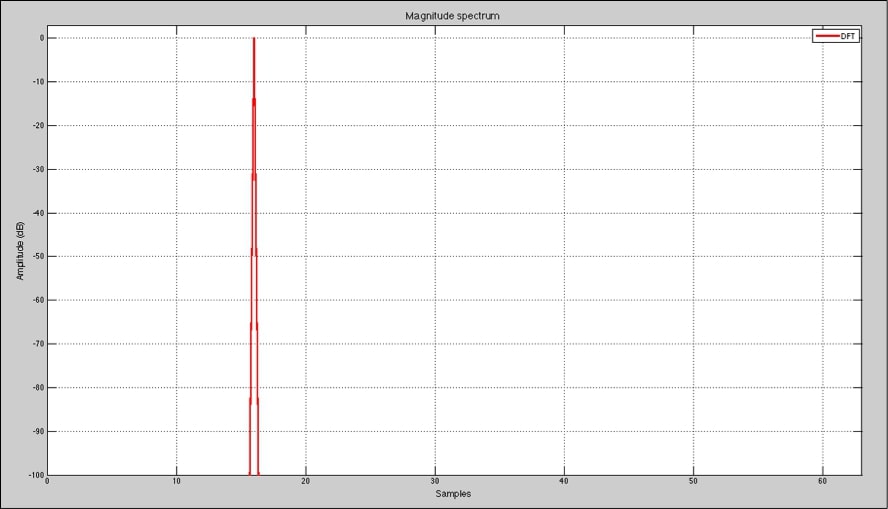
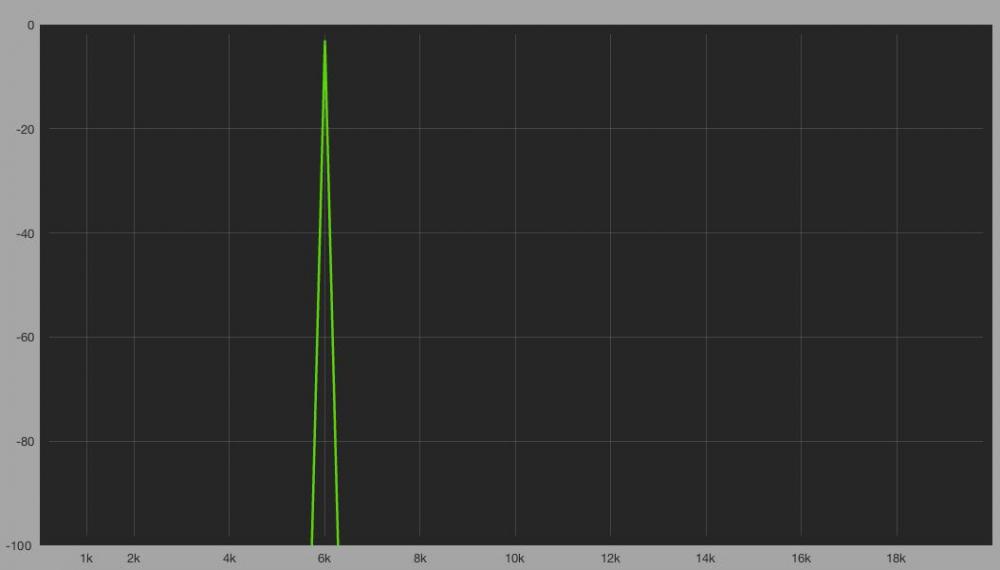
Del mismo modo que anteriormente, si la señal de entrada no coincide con un múltiplo de la frecuencia de resolución, el analizador tiene que repartir la energia entre las frecuencias colindantes:
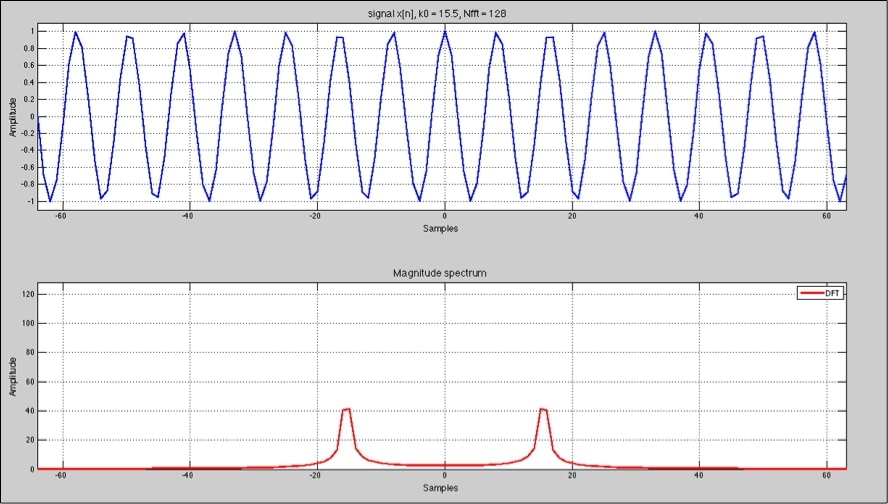
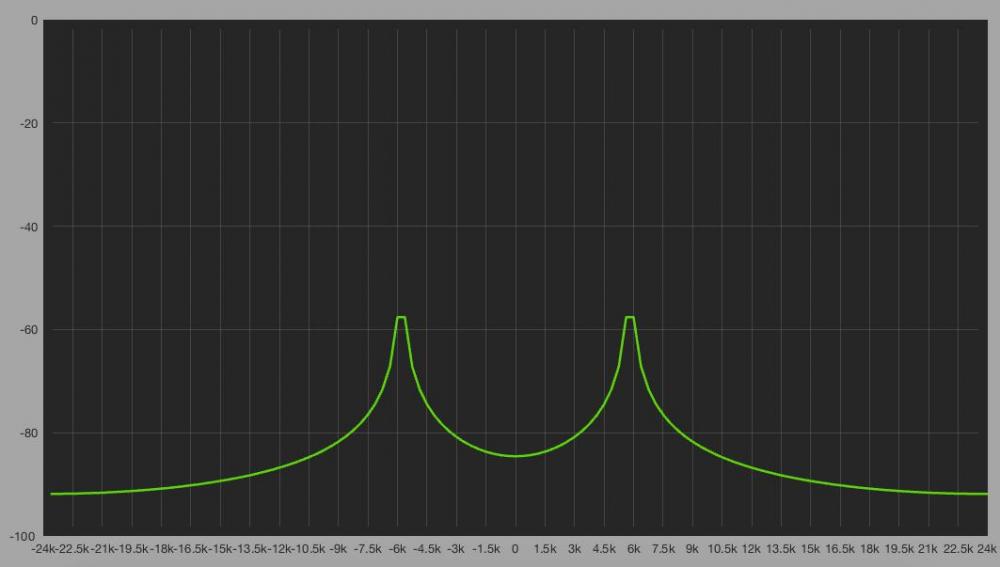
En este ejemplo, la frecuencia contiene 15.5 ciclos por lo tanto, podemos observar como aparecen dos frecuencias, parte positiva y negativa y como el analizador tiene que repartir la amplitud del valor de la señal entre los valores de frecuencia más cercanos.
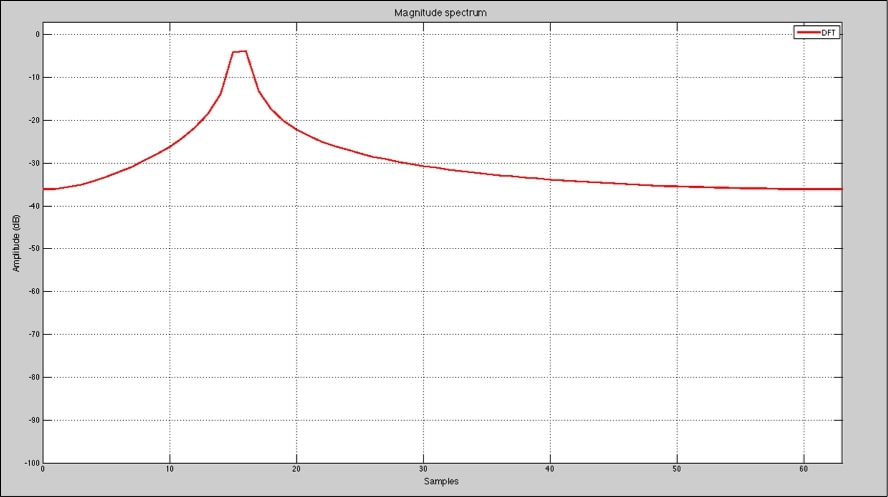
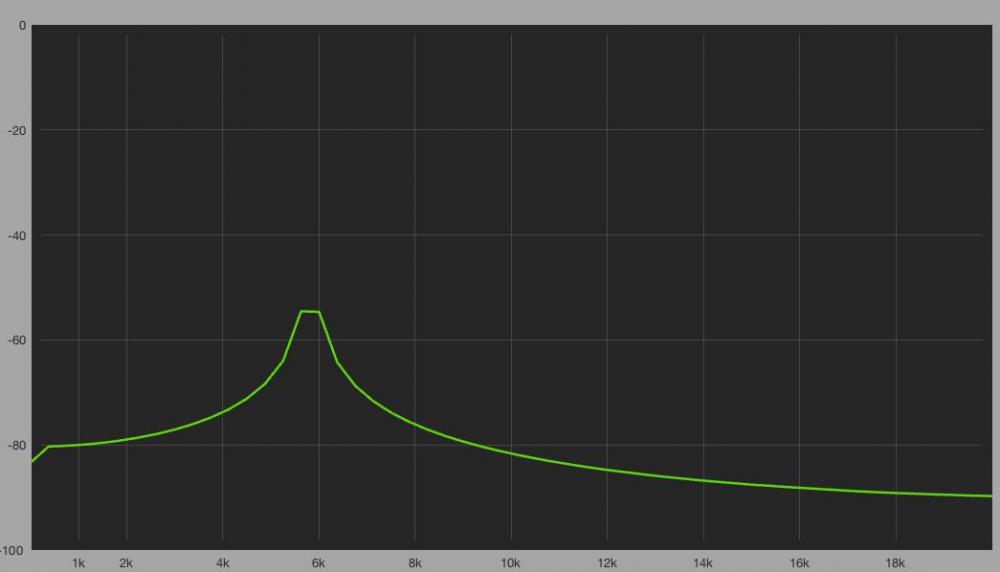
Como vemos, en ambas respuestas el resultado de la medición no es del todo correcto, a pesar que aproxima el valor de frecuencia a la señal analizada, no muestra correctamente la amplitud y nos muestra energía en frecuencias que no están presentes en la señal. Para aproximar a la frecuencia correcta los analizadores utilizan funciones de ventana. Hablaremos de ello en un próximo artículo.
Inverse DFT
Una de las grandes propiedades de la DFT es que es invertible, es decir, que podemos reconvertir la señal en el dominio temporal a partir de su respuesta espectral:
La operación es similar a la DFT, pero en este caso no multiplicamos por una exponencial negativa y normalizamos el resultado por la inversa del tamaño de la DFT.
Aunque ambas ecuaciones son muy parecidas, conceptualmente son muy diferentes, mientras la DFT realiza el análisis de una señal, la IDFT realiza la síntesis, es decir, reconstruimos la señal a partir de su espectro.
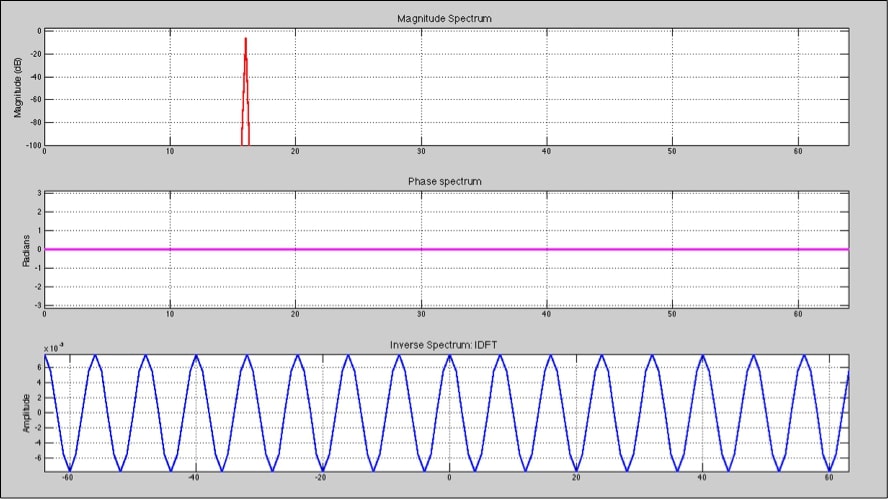
En el proceso de análisis al igual que mostramos la respuesta espectral también podríamos mostrar su respuesta de fase, pero para nosotros no es importante conocer la fase absoluta de una señal cuando analizamos sistemas, estamos interesados en conocer la fase relativa entre distintos elementos. Pero para la reconstrucción de una señal sí debemos tenerla en cuenta.
Por otro lado, en el caso de señales reales no necesitamos conocer el espectro completo, como sabemos que éste es simétrico, es suficiente con utilizar la parte positiva del mismo y computar su conjugado.
Limitaciones de la DFT
Como hemos podido comprobar el tamaño de la DFT determina la frecuencia de resolución, aunque esto no es del todo cierto, como veremos en el siguiente articulo, depende del tamaño del fragmento analizado, o lo que es lo mismo del tamaño de ventana. En estos ejemplos estamos usando el mismo tamaño de DFT que de ventana, por lo tanto asumimos que son lo mismo.
La frecuencia de resolucion determina que frecuencias pueden ser detectadas por el analizador, todas aquellas que se encuentren por debajo de la frecuencia de resolución no serán analizadas.
Analicemos un ruido aleatorio
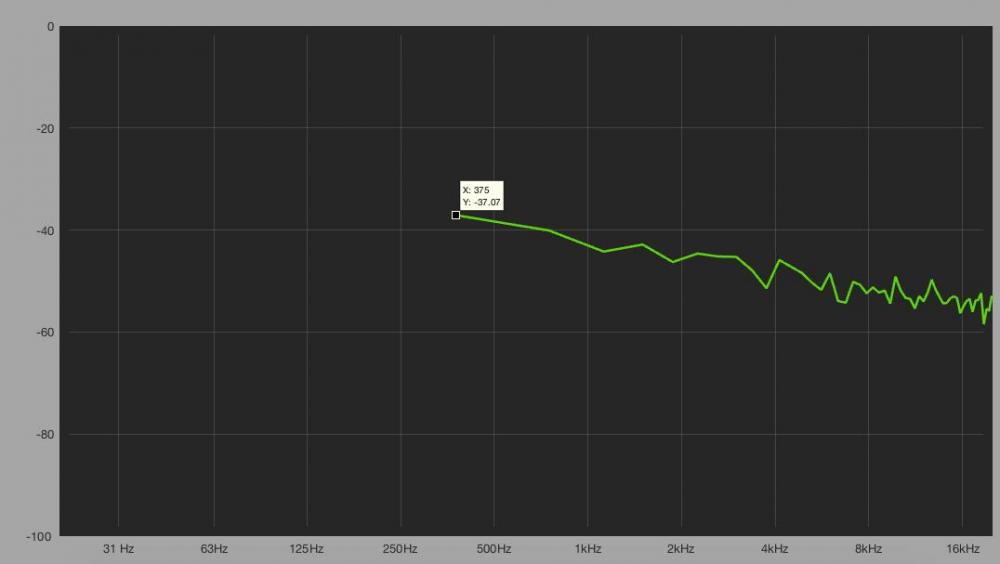
Fijémonos, como al visualizar la escala de frecuencia en modo logarítmico, con un tamaño de DFT de 128 muestras y una frecuencia de muestreo de 48kHz no podemos visualizar nada por debajo de 375Hz.
Nuestros analizadores utilizan estos cálculos para obtener los datos en frecuencia, pero en su implementación rápida, la transformada rápida de Fourier (FFT), que permite, siempre y cuando el tamaño de la DFT sea una potencia de 2, reducir el numero total de cálculos de N2 a N log2N .
La frecuencia de resolución lleva implicitamente asociada otra variable, la constante de tiempo (TC). La constante de tiempo, que no es más que la inversa de la recuencia de resolución, determina que espacio de tiempo es capaz de visualizar el analizador. Del mismo modo, todo aquello que quede fuera de la constante de tiempo será invisible para él.
Aunque pueda parecer en el proceso de medición de una señal, desde el punto de vista del tecnico de sonido, que la frecuencia de resolución y por lo tanto el espectro de la señal es lo importante, la contante de tiempo tiene un valor decisivo en el análisis cuando manipulamos la información para visualizar un espectrograma.
Una constante de tiempo pequeña nos va a proporcionar un buen detalle del tiempo en el cual suceden las cosas, por ejemplo, el tiempo de las reflexiones, pero una constante de tiempo pequeña nos aportará una muy pobre resolución frecuencial. Este es un cuello de botella en el mundo del análisis, tamaños grandes de FFT implican buena resolución a cambio de una mala resolución temporal, por el contrario, tamaños pequeños de FFT nos aportan una pobre visión de lo que ocurre en frecuencia a cambio de un buen detalle de lo que ocurre a través del tiempo.
El tamaño de FFT adecuado es aquel que nos permite visualizar lo que queremos conocer.
Bibliografía
Audio signal Processing for music aplications, Coursera, Stanford and UPF University, https://class.coursera.org
Más artículos de Pepe Ferrer aquí
¿Qué te ha parecido el artículo sobre la Representación Espectral? Lee más REPORTAJES DE OPINIÓN